Диаграммы направленности антенн с фазированной решеткой (часть 6) - боковые лепестки и сужение

Эта шестая статья завершает серию диаграмм диаграмм направленности антенн с фазированной решеткой, в которой обсуждаются боковые лепестки антенны и эффект сужения по решетке.
Ранее в этой серии, мы введены поэтапно - массив концепции, beamsteering, и массив усиления. Затем мы представили концепции лепестков решетки и косоглазия луча. В этой заключительной части мы обсудим антенну боковых лепестков и на эффект от сужающихся через в массив.

Сужение это просто манипуляция от амплитуды вклада в качестве отдельного элемента к в общей антенны ответ. Ранее в серии не применялось сужение, и первые боковые лепестки составляли –13 дБн, как показано на рисунках. Сужение обеспечивает способ снижения антенны боковых лепестков на каком - то счет к в антенне усиления и главное - лепесток лепесток. После в введения в сужающийся, мы подробно остановиться на нескольких точках относительно антенны усиления.


Преобразование из в прямоугольной функции в одном домене , чтобы в синк функции в другом домене появляется в различных формах в области электротехники. Наиболее распространенная форма - это когда прямоугольный импульс во времени излучает спектральное содержание функции sinc. Он также используется в обратном направлении, когда широкополосные приложения преобразуют широкополосный сигнал в узкий импульс во времени. Антенны с фазированной антенной решеткой обладают аналогичным свойством: прямоугольное взвешивание вдоль плоской оси решетки излучает диаграмму направленности, следующую за функцией sinc .

Для приложений с этим свойством боковые лепестки функции sinc проблематичны, так как первый боковой лепесток составляет всего –13 дБн. Рисунок 1 иллюстрирует этот принцип.
Сужение (или утяжеление)

Решением проблемы боковых лепестков является применение взвешивания прямоугольного импульса. Это является общим в быстрых преобразованиях Фурье ( БПФ), и сужающиеся варианты в фазированных решетках являются непосредственно аналогичны Весоизмерительным применяются в FFTs. К сожалению, недостаток взвешивания состоит в том, что боковые лепестки уменьшаются за счет расширения главного лепестка. Некоторые примеры весовых функций показаны на рисунке 2 .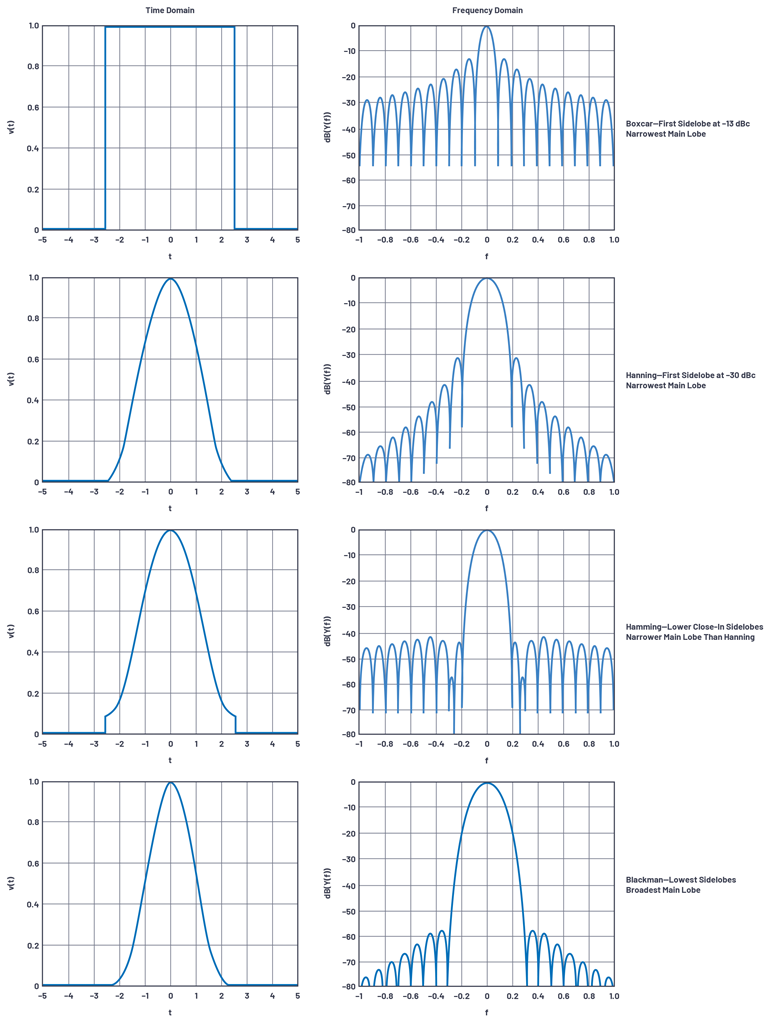



Форма волны и аналогия с антенной

Преобразование домена от времени к частоте достаточно рутинно, поэтому для большинства инженеров-электриков становится естественным его визуализация. Однако для инженеров, плохо знакомых с фазированными решетками, сначала может быть неочевидно, как использовать аналогию для диаграмм направленности антенн . Для этого мы заменяем сигнал во временной области возбуждением в полевой области , а выходной сигнал в частотной области заменяем на пространственную область.

Временная область → область поля

v ( t ) - напряжение как функция времени
E ( x ) - напряженность поля как функция положения в апертуре.
Частотная область → пространственная область

Y ( f ) - спектральная плотность мощности как функция частоты
G ( q ) - коэффициент усиления антенны как функция угла
Рисунок 3 иллюстрирует принцип. Здесь мы сравниваем излучаемую энергию для двух разных весов, приложенных к решетке. Рисунки 3a и 3c иллюстрируют область поля. Каждая точка представляет собой амплитуду одного элемента в этом массиве N = 16. Вне от антенны, есть не кого не излучаемой энергии, и излучение начинается на антенном края. На рис. 3а поле резко меняется, а на рис. 3с наблюдается постепенное увеличение по мере удаления от края антенны. Результирующее воздействие на излучаемую энергию показано на Рисунке 3b иРисунок 3д соответственно.




В следующих разделах мы введем два дополнительных члена ошибки, которые влияют на характеристики диаграммы направленности антенны. Первый - это взаимная связь. В этой статье мы просто признаем проблему и объем электромагнитного моделирования, использованного для количественной оценки воздействия. Вторая квантования боковых лепестков из - за , чтобы в конечном количестве битов в контроле фазового сдвига. Более подробно рассматриваются ошибки квантования, и количественно оцениваются боковые лепестки квантования .

Ошибки взаимной связи

Все обсуждаемые здесь уравнения и графики коэффициентов решетки предполагают, что элементы идентичны и имеют одинаковую диаграмму направленности. На практике это не так. Одна из причин касается взаимной связи, то есть связи между соседними элементами. Эффективность излучения элемента может значительно измениться, когда он широко разделен в массиве по сравнению с тем, когда он расположен более близко. Эти элементы на краю этого массива имеют различную окружающую среду , чем на элементах в в середине части в массиве.

F urthermore, как управляемый луч, он изменяет взаимное сцепление между элементами. Все эти эффекты создают в дополнительной ошибке термин для быть , приходящимся на от с проектировщиком антенны и, на практике, много усилий тратятся электромагнитными тренажерами , чтобы характеризовать радиационные эффекты при этих условиях.

Разрешение по углу луча и боковые лепестки квантования

Другое практическое ухудшение фазированной антенной решетки связано с конечным разрешением блока временной задержки или фазовращателя, используемого для управления лучом. Обычно это управляется цифровым способом с дискретными временными ( или фазовыми ) шагами. Но как определить разрешение или количество битов, необходимых для достижения целевого качества луча?

В противоположности к общим заблуждениям, луч - угол разрешение не эквивалентно к разрешению фазовращателей. В уравнении 1 мы находим это соотношение:
Клик
Мы можем выразить это в терминах из за фазовый сдвиг через по всей матрице с помощью подменено Tüting массива ширины D для расстояния элемента д. Если мы затем заменить на устройствах сдвига фазы для ΦLSB ДФА, мы можем приблизить разрешение луча угла. Для линейного массива с N элементами разнесены на половину длины волны, разрешение на угол луча показано в уравнении 2:
Клик
Это разрешение по углу луча вне линии визирования и описывает угол луча, когда одна половина решетки имеет фазовый сдвиг, равный нулю, а другая половина имеет фазовый сдвиг младшего разряда фазовращателя. Меньшие углы возможны, если менее половины массива запрограммировано на фазу LSB.

Рисунок 4 показывает зависимость луча угол для 30-элемента массива с помощью 2- х битную фазы переключения, как на этапе LSB , будет постепенно переключается на элементы из влево , чтобы справа через в массиве. Обратите внимание , что угол луча увеличивается до половины элементов не будут сдвинуты на LSB, а затем возвращается к нулю , когда все элементы находятся в LSB. Это имеет смысл когда угол луча изменяется из-за разницы фаз в решетке. Обратите внимание, что пиком этой характеристики является θ RES , как было рассчитано ранее.

Рисунок 5 участков • & thetas РЭС в качестве функции от диаметра массива ( при длине волны 2 / расстояния между элементом ) для различных разрешений фазосдвигающих. Это показываетчто даже очень грубый 2-битный фазовращатель с 90 ° LSB может достигнуть 1 ° разрешения для диаметра массива из 30 элементов.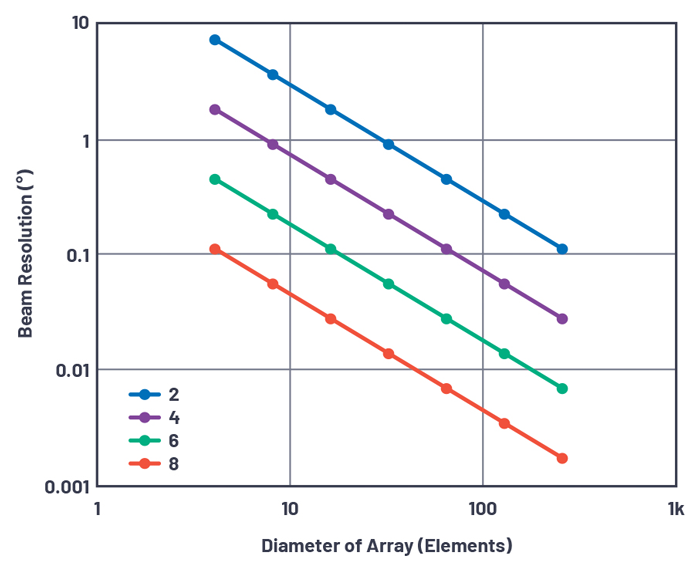

Решение уравнения 7 в части 2 , по крайней Л / 2 интервала 30 элементов, главный лепесток ширина луча составляет примерно 3,3 °, предполагая , что мы имеем достаточное разрешение , даже с этой очень грубой фазы сдвига. Итак, что же мы получаем для в фазе переключения , предлагая более высокое разрешение? Рисунок из аналогий между времени - выборки систем ( данные преобразователей ) и пространство - выборка система ( поэтапно - массив антенны ) , более высокое - преобразователь данных разрешения производит нижний шум квантования. С более высоким разрешением фазы / время сдвиг приводит в нижних квантовании боковых лепестков уровней ( QSLLs ) .

На рисунке 6 показаны настройки фазовращателя и фазовая ошибка для 2-битной 30-элементной линейной матрицы, описанной ранее, запрограммированной на угол разрешения луча θ RES . Половина массива установлена ​​на нулевой фазовый сдвиг, а другая половина установлена ​​на 90 ° LSB. Обратите внимание, что ошибка, разница между идеальным и фактическим квантованным сдвигом фазы, имеет пилообразную форму.

Диаграммы направленности антенны для той же антенны, повернутой на 0 ° и на угол разрешения луча, показаны на рисунке 7 . Наблюдается серьезная деградация шаблона из-за ошибки квантования фазовращателя.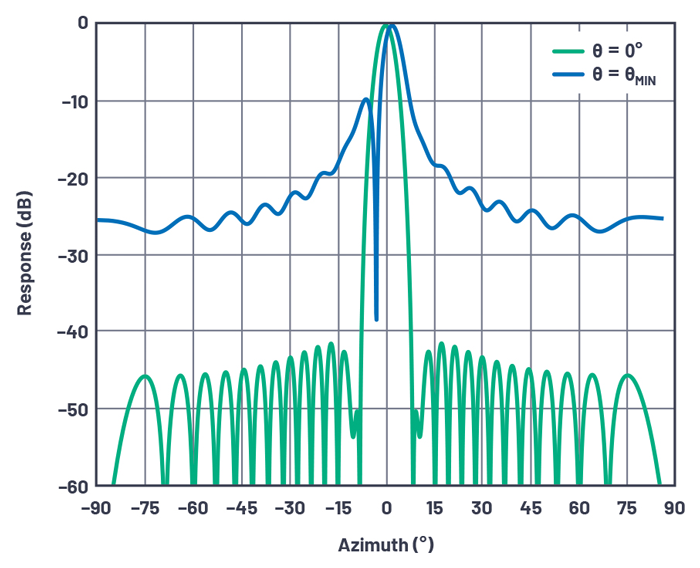

Боковые лепестки квантования наихудшего случая возникают, когда максимальная ошибка квантования возникает через апертуру, когда каждый другой элемент имеет нулевую ошибку, а сосед - младший бит / 2. Это представляет как максимально возможную ошибку квантования, так и максимальную периодичность ошибки по апертуре. Это условие показано для 2-битного 30-элементного случая на рисунке 8 .

Такие ситуации возникают при предсказуемых углах луча, как показано в уравнении 3:
Клик
где n <2 БИТОВ , а n нечетно. Для 2-битной системы это условие выполняется четыре раза между горизонтами, от ± 14,5 ° до ± 48,6 °. На рисунке 9 показана диаграмма направленности антенны для этой системы для n = 1, q = + 14,5 °. Обратите внимание на существенный боковой лепесток квантования –7,5 дБ при –50 °.

При углах луча, отличных от особых случаев, когда ошибка квантования последовательно равна 0 и LSB / 2, среднеквадратичная ошибка уменьшается, поскольку она распространяется по апертуре. Фактически, для уравнения угла ( уравнение 3 ) для четных значений n ошибка квантования равна нулю.

Если мы наносим относительный уровень самих высокого квантования боковых лепестков для различной фазы - устройства сдвига резолюций, некоторые интересные модели появляются. Фигура 10 показывает , наихудший QSLL для более 100-элемента линейного массива, использующего Хэмминга конусность , так что эти квантования боковые лепестки могут быть дифференцированы от классические боковые лепестки окон, обсуждаемые ранее в этом разделе.

10. На этом графике показаны боковые лепестки квантования в наихудшем случае в зависимости от угла луча для разрешения фазовращателя от 2 до 6 бит.

Обратите внимание, что при 30 ° вся ошибка квантования обращается в ноль, что может быть показано как следствие sin ( 30 ° ) = 0,5. Обратите внимание , что угол пучка наихудшего уровня для любого п-битной фаза устройства сдвига экспозиции нуля квантования ошибки при любом более высоком разрешении п. Можно увидеть описанные здесь углы луча для уровней боковых лепестков наихудшего случая, а также улучшение QSLL на 6 дБ на бит разрешения.

11. Показаны уровни боковых лепестков квантования в наихудшем случае в зависимости от разрешающей способности фазовращателя от 2 до 8 бит.

Максимальные уровни боковых лепестков квантования, QSLL, для разрешений фазовращателя от 2 до 8 бит показаны на рисунке 11 , который следует известному закону шума квантования для преобразователей данных:

или около 6 дБ на бит разрешения. При 2 битах уровни QSLL составляют около –7,5 дБ, что выше, чем классические +12 дБ для преобразователя данных, выбирающего случайный сигнал. Это несоответствие можно рассматривать как следствие периодически возникающей пилообразной ошибки, дискретизируемой через апертуру, где пространственные гармоники складываются по фазе. Обратите внимание, что QSLL не зависит от размера апертуры .

Заключительные комментарии

Теперь мы можем суммировать некоторые проблемы, с которыми сталкиваются антенные инженеры в отношении ширины луча и боковых лепестков:

Угловое разрешение требует узкого луча. Для узкого луча нужна большая апертура, для которой требуется много элементов. Кроме того, луч расширяется при отклонении от оси визирования, поэтому необходимы дополнительные элементы для сохранения ширины луча при увеличении углов сканирования.
Может показаться возможным увеличить расстояние между элементами для увеличения общей площади антенны без добавления дополнительных элементов. Это сузит луч, но, к сожалению, приведет к появлению лепестков решетки, если элементы расположены равномерно. Уменьшение угла сканирования, наряду с апериодическими решетками, реализующими намеренно рандомизированную структуру элементов, можно исследовать, чтобы использовать увеличенную площадь антенны, минимизируя проблему лепестков решетки.
Боковые лепестки - еще одна проблема, которую, как мы узнали, можно уменьшить, уменьшив усиление массива по направлению к краям. Однако сужение происходит за счет расширения балки, что опять же требует большего количества элементов. Разрешение фазовращателя может привести к появлению боковых лепестков квантования, которые также необходимо учитывать в конструкции антенны. Для антенн, реализованных с фазовращателями, явление скоса луча вызывает угловой сдвиг в зависимости от частоты, ограничивая полосу пропускания, доступную для высокого углового разрешения.
На этом мы завершаем серию из шести частей о диаграммах направленности фазированных антенных решеток. Мы ввели наведение луча , коэффициент решетки и усиление антенны , а затем исследовали недостатки лепестков решетки и косоглазия луча. Наконец, мы обсудили ошибки сужения и квантования. Намерение направлено не для антенных проектных инженеров , свободно владеющих в электромагнитной и излучающем элементе конструкции, но довольно большое число из инженеров в смежных дисциплинах работающего на фазированных решетках кому может быть полезно интуитивно понятное объяснение различных воздействий, влияющих на общие характеристики диаграммы направленности антенны .

Питер Делос - технический руководитель, Боб Бротон - технический директор компании Analog Devices в области аэрокосмической и оборонной промышленности, а Джон Крафт - старший инженер по полевым приложениям в Analog Devices .

Рекомендации

Баланис, Константин А. Теория, анализ и конструкция антенн . Третье издание. Wiley, 2005.

Mailloux, Robert J. Справочник по антеннам с фазированной решеткой . Второе издание. Artech House, 2005 год.

О'Доннелл, Роберт М. « Разработка радиолокационных систем: Введение ». IEEE, июнь 2012 г. Skolnik, Merrill. Справочник по радарам. Третье издание. Макгроу Хилл, 2008.